ضرب ذهنی اعداد در یازده ، ریاضیات سریع محاسباتی تراخنبرگ

با ضرب ذهنی اعداد در یازده تراختنبرگ ، دیگر هیچ کسی را نخاهید یافت که از ریاضی متنفر باشید . کافیست امتحان کنید و این روش ها را تمرین کنید ، روش هایی که سالهاست در کشور های اروپایی برای ضرب ذهنی اعداد در یازده اکادمیک شده و به سبب همین موضوع و محاسبات ذهنی ، سویسی ها در بانکداری سرامد دنیا شده اند. تراختنبرگ این روش ها را در زندان های نازی ها اختراع کرد و دنیارا متحول کرد ، امیدوارم روش های ذهنی تراختنبرگ برای شما نیز مفید باشد.
در ابتدا ، می خواهیم با محتوای این روش آشنا شویم. نخستین موضوع بحث، شیوه جديد انجام عمل ضرب است: می خواهیم عمل ضرب را بدون از برداشتن جدول ضرب انجام دهیم. ناممکن به نظر می رسد ؟ نه تنها ممکن است،بلکه بسیار اسان می باشد. البته باید این توضیح را هم بدهیم که با استفاده از جدول ضرب مخالف نیستیم. بیشتر اشخاص جدول ضرب را خوب بلدند؛ به عبارت دیگر همه آن را از بر کرده اند و فقط ممکن است در چند مورد از ضرب ها دچار تردید شوند. ممکن است کسی در مورد هشت هفت تا ، یا شش نه تا قدری شک کند ولی اعداد کوچکتری مثل چهار پنج تا ، برای همه بسیارر ساده می باشد ومانند اب خوردن است. ما با استفاده از این معلوماتی که بزحمت حاصل شده، موافقیم. منظور ما در اینجا انسجام بخشیدن به آن است. راجع به این موضوع دوباره در همین مقاله سخن خواهیم گفت. اکنون می خواهیم برخی عملهای ضرب را بدون استفاده از جدول و بصورت ذهنی انجام دهیم.

مزایای ضرب ذهنی اعداد در یازده (تراختنبرگ):
1-با فراگیری این روش شما به راحتی در امور روزانه خود سطح بیشتری از ظرفیت مغزی خود را در اختیار داشته باشید.
2-ارتباط بین دو نیم کره را افزایش می دهد و موجب پیشرفت فرد در تمامی زمینه های زندگی و تحصیلی می شود.
3-با فعالیت های ذهنی ریاضی ذهن شما ماننده یک ماشین حساب می شود و مانند ساعت کار میکند.

در ابتدا از ساده ترین این روش ها اغاز میکنیم و در هر مقاله به طور جداگانه به روش های پیشرفته تر و قواعد دیگر این نو از ریاضیات سریع میپردازیم.
از ضرب اعداد در یازده شروع می کنیم ، و روش کار را بصورت دستور هایی یادداشت میکنیم:

ضرب ذهنی اعداد در یازده:
1. آخرین عدد مضروب (عددی که در یازده ضرب می شود) را به عنوان رقم سمت راست جواب، می نویسیم.
۲. هر عدد متوالی از مضروب با همسایه طرف راست آن، جمع می شود.
٣. اولین عدد مضروب، رقم سمت چپ جواب می شود. این آخرین مرحله کار است.

در روش تراختنبرگ، مثل روش ضرب معمولی، رقم های جواب یکی یکی، از راست به چپ نوشته می شود مثال ساده برای درک بهتر این روش می زنم: 633 ضرب در 11

با استفاده از این دستورها ، جواب را یک رقم، یک رقم، از راست به چپ، زیر 633 می نویسیم. از این پس برای انجام کار به همین صورت عمل می کنیم. ستاره های بالای مضروب در این مثال نشان میدهند که در هر مرحله از محاسبه، با کدام رقمها سرو کار داریم. حالا دستورها را به کار می بندیم .

دستور اول : آخرین رقم 633 را به عنوان رقم سمت راست می نویسیم.

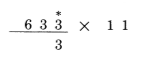
دستور دوم : هر رقم متوالی از633 را با همسایه طرف راست آن جمع می کنیم،3 به علاوه 3 می شود 6 :

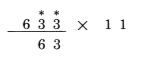
این دستور را دوباره به کار می بندیم، 6 بعلاوه3 میشود 9:

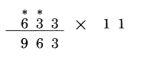
دستور سوم : اولین رقم 633 یعنی 6، رقم سمت چپ جواب می شود

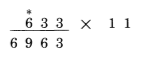
پس جواب 6963 است.

در مورد اعداد طولانی تر ضرب ذهنی اعداد در یازده باز هم ذهنی به همین روش عمل می کنیم. دستور دوم که «هر رقم متوالی از مضروب به همسایه طرف راست آن افزوده می شود ، در مثال بالا دوبار به کار رفته است در عدد های طولانی تر چند بار آن را به کار می بریم.
مانند : 721324 ضرب در 11:

دستور اول آخرین رقم 721324 به عنوان رقم سمت راست جواب نوشته می شود :

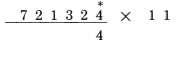
دستور دوم هر رقم متوالی از 721324 با همسایه طرف راست آن، جمع می شود :
2 به علاوه 4 می شود 6
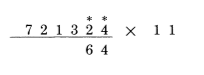3به علاوه 2 می شود 5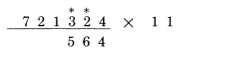
1به علاوه 3 می شود 4

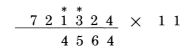
2به علاوه 1 می شود 3

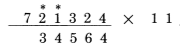
7به علاوه 2 می شود 9

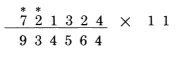
دستور سوم : اولین رقم 721324، رقم سمت چپ جواب می شود

پس جواب 7934564 است.

همانطور که می بینید، هر رقم از عدد طولانی دوبار به کار می رود . یک بار به عنوان «عدد » و سپس، در مرحله بعد، به عنوان «همسایه» به کار می رود . در مثال اخیر، رقم ۱ (از مضروب) هنگام دادن رقم 4 از جواب، عدد بود ، ولی در مرحله بعد، وقتی با ۲ جمع می شد تا رقم ۳ را بدهد، «همسایه» به شمار می آمد.

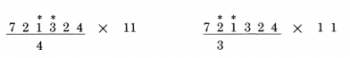
به جای استفاده از این سه دستور، می توانیم یک دستور را در مفهوم طبیعی و عادیش به کار ببریم. این دستور چنین است: «با همسایه جمع کن». ابتدا باید صفری جلوی عدد داده شده بنویسیم یا فرض کنیم صفری جلویش هست. سپس دستور جمع کردن با همسایه را به نوبت در مورد همه رقم های عدد داده شده اجرا می کنیم.

این مثال نشان می دهد که چرا باید جلوی مضروب صفر بگذاریم.در روش ذهنی این صفر به ما یاد آوری می کند که کار را زودتر قطع نکنیم. اگر صفر را جلوی عدد ننویسیم، ممکن است فراموش کنیم که رقم 6 را در آخر جواب بنویسیم و در نتیجه خيال کنیم که جواب همان ۹۶۳ است. جواب همیشه یک رقم طولانی تر از عدد مفروض است، و صفر جلوی عدد موجب رعایت این نکته می شود .

حالا خودتان مثالی حل کنید: 441362 ضرب در 11 ، ان را به صورت مناسب بنویسید.

اگر کار را با ۲ شروع کنید که محل درست شروع است، و مرحله به مرحله به سمت چپ بیایید و در هر مرحله، همسایه را با رقم جمع کنید ، باید به جواب درست برسید که 4854982 است.

گاه در جمع کردن یک رقم با همسایه اش، عددی دو رقمی به دست می آید، مثلا ۵ با ۸ که ۱۳ می شود . در این حالت ۳ را می نویسید و یک را همان طور که در حساب دیده اید به عنوان ده بر یک نگاه می دارید . اما خواهید دید که در روش تراختنبرگ هیچ وقت لازم نمی شود عدد بزرگی را نگاه دارید. اگر رقمی نگاه داشته شود یا ۱ است یا در مراحل بعدتر احيانا ۲. این تفاوت در موقع حل مسائل پیچیده تأثير زیادی دارد.

کافی است برای «ده بر یک»، از یک نقطه و برای «بیست بر دو» که کمتر پیش می آید از دو نقطه استفاده کنیم.

یک مثال برای ضرب ذهنی اعداد در یازده : 715624 ضرب در 11. اول آن را به صورت زیر بنویسید:

زیر رقم ۵ از این عدد یک «ده بر یک» خواهید داشت.

جواب درست مسئله، 7871864 است.

ضرب ذهنی اعداد در یازده در حالت خیلی خاصی از عددهای طولانی که با 9 شروع می شوند و بعد از آن هم رقم بزرگی مثل 8 دارند، مثلا در مورد 98,834 ممکن است در آخرین مرحله یک ۱۰ داشته باشیم. مثال:
با من همراه باشید تا د ر مقاله بعدی ، روش های ضرب اعداد در 12 را برسی کنیم.
میتونید تمرین هاتون رو انجام دهید و سوالاتون رو از من بپرسید در بخش کامنت ها*-* .